# Dépendances pour l'analyse des données et les représentations graphiques.
library(magrittr)
library(ggplot2)
library(dplyr)
library(IAM)
library(parallel)
library(beepr)Le modèle bio-économique IAM a été développé notamment pour permettre d’accompagner le développement des plans de gestion des pêcheries et d’explorer les conséquences biologiques et socio-économiques de différents scénarios de TAC et quotas et de transition vers le Rendement Maximum Durable - RMD (ou Maximum Sustainable Yield - MSY).
Ce document présente la mise en œuvre avec le modèle IAM de scénarios de TAC et quotas correspondant à différents chemins de transition vers le \(F_{msy}\) (différentes valeurs de TAC constants permettant l’atteinte du FMSY plus ou moins rapidement).
L’ensemble des simulations présentées dans l’exemple sera réalisé
avec le jeu de donnée example Ifremer composé de 7
flottilles et 3 espèces dynamiques dont une espèce à dynamique SS3. Les
simulations prennent en compte la variabilité du recrutement et ses
conséquences en termes de probabilité d’atteinte du FMSY. Dans ce cadre,
une réplication de valeur N sera réalisée à partir du jeu de donnée
exemple.
Attention ce document lance de nombreuses simulations \((1 + n_{TAC})\cdot N\) et prend donc un temps long à simuler (plusieurs dizaines de minutes).
data("IAM_input_2009")
summary(IAM_input_2009)
#> My Input (IAM input) :
#> Simulation of 3 dynamic species, 19 static species and 7 fleet
#> Simulation start in 2009 and end in 2020 (12 steps)
#>
#> ------------------------------------
#> Dynamic Species | Model | Ages |
#> ARC | XSA | 0 to +gp |
#> COR | XSA | 2 to +gp |
#> DAR | SS3 | 0 to +gp |
#> ------------------------------------
#> Fleet | nbv |
#> Alis | 24 |
#> Antea | 36 |
#> Atalante | 15 |
#> Haliotis | 5 |
#> Marion_Dufresne | 9 |
#> Pourquoi_pas | 18 |
#> Thalassa | 60 |L’objet argument est laissé tel quel lors de l’utilisation de l’interface et sera édité à la main plus tard pour chaque scénario.
# Cette ligne ouvre une interface via une app shiny.
IAM_argum_2009 <- IAM.args(IAM_input_2009)Cela revient à initialiser un objet de classe iamArgs
sans passer par l’interface avec la commande suivante :
IAM_argum_2009 <- IAM.input2args(IAM_input_2009)Scénario statu quo
Afin de pouvoir comparer l’effet de chaque scénario, il nous faut un scénario de départ dans lequel les mesures de Gestion ne s’imposeront pas.
Dans un premier temps, les dynamiques de recrutements ainsi que des
éléments de paramétrage du module économique sont définies. On va pour
cela éditer l’objet IAM_argum_2009.
# Module SR
# Add noise to COR recruitment
IAM_argum_2009@arguments$Recruitment$COR$wnNOISEmodSR <- 0.203
IAM_argum_2009@arguments$Recruitment$COR$noiseTypeSR <- 2 # Log-normal
IAM_argum_2009@arguments$Recruitment$COR$typeMODsr <- "Hockey-Stick"
IAM_argum_2009@arguments$Recruitment$COR$parAmodSR <- 2539.5
IAM_argum_2009@arguments$Recruitment$COR$parBmodSR <- 9679
# Module EcoDCF
IAM_argum_2009 <- IAM.editArgs_Eco(IAM_argum_2009, dr = 0.04, perscCalc = 1)
# Module Gestion
mfm <- with(IAM_input_2009@input$Fleet,{
(effort1_f_m * effort2_f_m * nbv_f_m) / as.vector(effort1_f * effort2_f * nbv_f)
})
mfm[is.na(mfm)] <- 0
IAM_argum_2009 <- IAM.editArgs_Gest(IAM_argum_2009, active = FALSE,
delay = 1, mfm = mfm)
# Module Scenario
IAM_argum_2009 <- IAM.editArgs_Scenar(IAM_argum_2009) # desactivate scenario
summary(IAM_argum_2009)
#> My Input (IAM argument) :
#> Simulation of 3 dynamic species, 19 static species and 7 fleet
#> Simulation start in 2009 and end in 2020 (12 steps)
#>
#> =======================================================================================
#> SR module | Stock Recruitment | Noise | Proba |
#> ---------------------------------------------------------------------------------------
#> Species | function : param A ; param B ; param C | Type : sd | Type |
#> ARC (XSA) | Mean 3.641e+07 0.00e+00 0.00e+00 | Norm | 0.00e+00 | . |
#> COR (XSA) | Hockey-Stick 2.540e+03 9.68e+03 0.00e+00 | LogN | 2.03e-01 | . |
#> DAR (SS3) | not activated 0.000e+00 0.00e+00 0.00e+00 | Norm | 0.00e+00 | . |
#> ---------------------------------------------------------------------------------------
#>
#> The Gestion module is not active.
#>
#> ============================================================
#> Economic : PerscCalc = 1 ; dr = 0.040 | No replicates |
#> ------------------------------------------------------------
#>
#> The Scenario module is not active.Selection des différents TACs.
La recherche du TAC pour atteindre le \(F_{msy}\) se fait en simulant plusieurs scénarios correspondant à différentes valeurs de TACs simulées.
Les scénarios sont simulés avec \(N\) réplicats, correspondant à la variabilité du recrutement.
Les valeurs de \(N\), \(F_{msy}\) et \(TAC\) sont fixées ici :
N <- 50
Fmsy <- 0.26
TACS <- seq(3200, 5600, by = 400)350 simulations seront donc effectuées. La simulation du scénario Statu Quo est codée comme suit :
# Statu quo
SQ <- replicate(N, {
IAM::IAM.model(objArgs = IAM_argum_2009, objInput = IAM_input_2009)
})
SQl <- lapply(1:N, function(y) {
IAM.format(SQ[[y]], name = c("Fbar", "SSB", "L_et"),
sim_name = "SQ", n = y)
})
SQ <- do.call(rbind, SQl)Afin de simplifier le code, seules les variables biologiques seront extraites et représentées. Pour cela, la fonction suivante est utilisée :
#' Function for simulation under TAC
#' @param x TAC value
#' @param argum iamArgs object
#' @param input iamInput object
#' @param N Number of replicates
#'
#' @return formated table of class iam_formtbl that regroup values
#' for N simulation under a scenario. Only Fbar, SSB and L_et
#' variables are extracted.
simultac <- function(x, argum, input, N){
argum_int <- IAM.editArgs_Gest(argum, type = "x", active = TRUE,
tac = c(NA, NA, rep(x, 10)) )
sim <- replicate(N, {
IAM::IAM.model(objArgs = argum_int, objInput = input, mOTH = 1)
})
siml <- lapply(1:N, function(y) {
IAM.format(sim[[y]], name = c("Fbar", "SSB", "L_et"),
sim_name = as.character(x), n = y)
})
sim <- do.call(rbind, siml)
return(sim)
}De même, des modifications du paramètrage sur le module Gestion ont
lieu en commun pour tout les scénarios suivants. Ces modifications sont
regroupées ici avec la selection de la variables d’ajustement
(Nb trips), la cible (TAC), l’espèce
concernées (COR), un délais avant l’application de la
mesure de gestion (2 ans) et comment s’applique la modulation de
l’effort (multiplicatif borné entre 1e6 et -100)
IAM_argum_2009_TAC <- IAM.editArgs_Gest(
IAM_argum_2009, active = FALSE, control = "Nb trips", target = "TAC",
espece = "COR", delay = 2,
type = "x", bounds = c(1e6, -100),
tac = c(NA, NA, rep(3600, 10)))
# 09, 10, 2011:2020
TACS # TACS values to remember
#> [1] 3200 3600 4000 4400 4800 5200 5600
# Warning ! Code run for long time.
x <- Sys.time()
cl <- makeCluster(detectCores()-1)
invisible(clusterEvalQ(cl,library(IAM)))
res <-parLapply(cl, as.list(TACS), simultac,
IAM_argum_2009_TAC, IAM_input_2009, N)
stopCluster(cl)
res <- do.call(rbind, c(res, list(SQ)))
print(Sys.time() - x)
#> Time difference of 3.995515 minsReprésentations graphiques
On peut aisement comparer les différents scénarios en utilisant les fonctions graphiques.
COR <- res %>%
filter(species == "COR") %>%
IAM.format_quant(., probs = c(.025, .975))
COR %>%
ggplot(aes(x = year, y = median)) +
facet_grid(variable ~ sim_name, scales = "free_y") +
geom_ribbon(aes(ymin = quant1, ymax = quant2), fill = "lightblue") +
geom_line() +
geom_line(aes(y = value), linetype = "dotted") +
geom_vline(xintercept=2011, linetype = "dotted") +
IAM_theme() +
NULL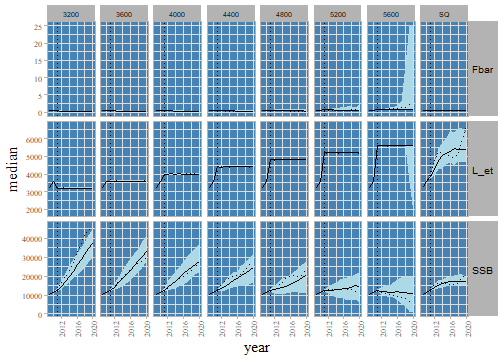
COR variables for different TAC scenarii. 50 runs.
line_data <- data.frame(xintercept = c(2011, 2015),
Lines = c("Scenarii start", "Target Fmsy"),
linetype = c("dotted", "dashed"),
stringsAsFactors = FALSE)
Proba <- res %>%
filter(species == "COR") %>%
group_by(.data$sim_name, .data$variable, .data$year) %>%
summarize(Pfmsy = sum(.data$value <= Fmsy) / length(unique(n)) * 100,
.groups = "keep") %>% ungroup()
Proba %>%
filter(variable == "Fbar") %>%
ggplot(aes(x = year, y = Pfmsy, color = as.factor(sim_name)))+
geom_line() +
geom_vline(xintercept= line_data$xintercept, linetype = line_data$linetype) +
annotate("text", line_data$xintercept, 100, hjust = -.25,
label = line_data$Lines) +
scale_colour_discrete(name ="TAC constant") +
NULL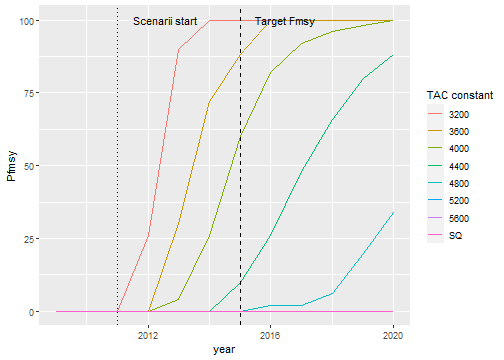
Fmsy Probability over 50 runs. Target Fmsy for COR species is : 0.26
filter(Proba, year == 2015, variable == "Fbar")
#> # A tibble: 8 x 4
#> sim_name variable year Pfmsy
#> <chr> <chr> <dbl> <dbl>
#> 1 3200 Fbar 2015 100
#> 2 3600 Fbar 2015 88
#> 3 4000 Fbar 2015 60
#> 4 4400 Fbar 2015 10
#> 5 4800 Fbar 2015 0
#> 6 5200 Fbar 2015 0
#> 7 5600 Fbar 2015 0
#> 8 SQ Fbar 2015 0
beepr::beep(3)TAC jusqu’au Fmsy.
On reproduit l’analyse précédente mais en changeant la cible des scénarios. Ainsi, on va ici viser un TAC jusqu’à atteinte d’un Fbar. On précise pour cela un \(Fbar\) cible et on réduit les bornes de recherche du multiplicateur \(\mu\).
IAM_argum_2009_TAC_fmsy <- IAM.editArgs_Gest(
IAM_argum_2009_TAC, active = FALSE, target = "TAC->Fbar",
type = "x", bounds = c(100, -100),
tac = c(NA, NA, rep(3600, 10)),
fbar = c(NA, NA, rep(Fmsy, 10)))
# 09, 10, 2011:2020
TACS # TACS values to remember
#> [1] 3200 3600 4000 4400 4800 5200 5600
# Warning ! Code run for long time.
x <- Sys.time()
cl <- makeCluster(detectCores()-1)
invisible(clusterEvalQ(cl,library(IAM)))
res <-parLapply(cl, as.list(TACS), simultac,
IAM_argum_2009_TAC_fmsy, IAM_input_2009, N)
stopCluster(cl)
res <- do.call(rbind, c(res, list(SQ)))
print(Sys.time() - x) # 50 -> 3 min
#> Time difference of 5.708266 minsReprésentations graphiques
Les représentations graphiques reprennent le même code que précédement.
COR <- res %>%
filter(species == "COR") %>%
IAM.format_quant(., probs = c(.025, .975))
COR %>%
ggplot(aes(x = year, y = median)) +
facet_grid(variable ~ sim_name, scales = "free_y") +
geom_ribbon(aes(ymin = quant1, ymax = quant2), fill = "lightblue") +
geom_line() + geom_point(size = .5) +
geom_line(aes(y = value), linetype = "dotted") +
geom_vline(xintercept=2011, linetype = "dotted") +
IAM_theme() +
NULL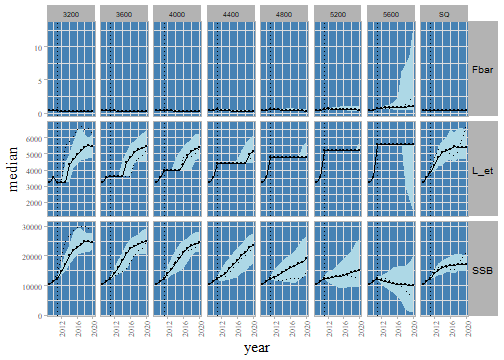
COR variables for different TAC scenarii. 50 runs.
Calcul de la probabilité d’atteindre le \(F_{msy}\)
On peut calculer la probabilité d’atteindre le \(F_{msy}\) comme le pourcentage de simulation ayant un \(F_{bar} < F_{msy}\).
line_data <- data.frame(xintercept = c(2011, 2015),
Lines = c("Scenarii start", "Target Fmsy"),
linetype = c("dotted", "dashed"),
stringsAsFactors = FALSE)
Proba <- res %>%
filter(species == "COR") %>%
group_by(.data$sim_name, .data$variable, .data$year) %>%
summarize(Pfmsy = sum(.data$value <= Fmsy) / length(unique(n)) * 100,
.groups = "keep") %>% ungroup()
Proba %>%
filter(variable == "Fbar") %>%
ggplot(aes(x = year, y = Pfmsy, color = as.factor(sim_name)))+
geom_line() +
geom_vline(xintercept= line_data$xintercept, linetype = line_data$linetype) +
annotate("text", line_data$xintercept, 100, hjust = -.25,
label = line_data$Lines) +
scale_colour_discrete(name ="TAC constant") +
NULL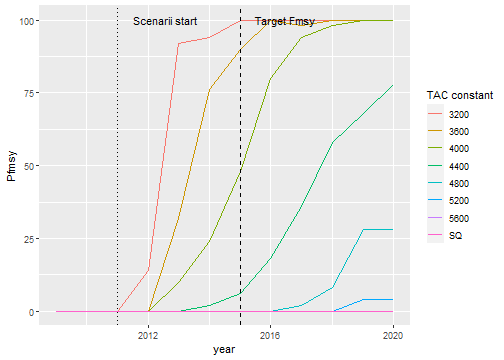
Fmsy Probability over 50 runs. Target Fmsy for COR species is : 0.26
filter(Proba, year == 2015, variable == "Fbar")
#> # A tibble: 8 x 4
#> sim_name variable year Pfmsy
#> <chr> <chr> <dbl> <dbl>
#> 1 3200 Fbar 2015 100
#> 2 3600 Fbar 2015 90
#> 3 4000 Fbar 2015 48
#> 4 4400 Fbar 2015 6
#> 5 4800 Fbar 2015 0
#> 6 5200 Fbar 2015 0
#> 7 5600 Fbar 2015 0
#> 8 SQ Fbar 2015 0
beepr::beep(3)