Utilisation IAM dans R (fr)

Le modèle bio-économique IAM a été développé dans l’optique d’être utilisable sous un environnement R (R Core Team 2021). L’outil est ainsi accessible par l’intermédiaire d’un package R intégrant un ensemble de méthodes couvrant toutes les étapes de la modélisation, de la phase de paramétrage à la restitution des sorties du modèle. Cette vignette traite des possibilités offertes par les outils du package, et de la manière dont on peut les utiliser pour procéder de manière relativement simple et rapide à des simulations et aux traitements des résultats.

Choix d’implémentation

Les choix d’implémentation du modèle IAM ont découlé d’exigences techniques fixées dans le but de maximiser la pérennité et la fonctionnalité du modèle. Elles portaient à la fois sur l’aspect purement technique du programme (rapidité, qualité des algorithmes,…), sur sa flexibilité (généricité et robustesse face à la multiplicité des configurations d’inputs prises en charge, diversité des scénarios proposés, choix des bases de données d’entrée, diversité des outils satellites au modèle proprement dit,…) ou encore sur son accessibilité (simplicité d’utilisation, logiciels gratuits et facilement téléchargeables, installation simple, méthodes à la fois génériques et paramétrables,…).

Le langage R réunit une grande partie de ces caractéristiques. C’est un logiciel libre et gratuit de traitement statistique, largement répandu à l’heure actuelle au sein de la communauté halieutique et qui offre l’avantage d’être relativement simple d’emploi. Il représente un environnement adéquat pour gérer des objets de paramétrage (notamment multidimensionnels, comme le sont ceux du modèle bio-économique). De surcroît, les sorties exportées en tant qu’objets R peuvent bénéficier des nombreuses fonctionnalités proposées par le logiciel (sorties graphiques, traitements statistiques,…).

Toutefois, il est apparu que le modèle deviendrait très rapidement exigeant en terme de temps calcul (algorithmes d’optimisation, beaucoup de variables, beaucoup de dimensions,…) et que l’utilisateur trouverait là la limite des possibilités offertes par R. La solution la plus évidente était de programmer le cœur du modèle en C++, et de laisser R piloter les routines, se contentant ainsi de gérer le paramétrage et le traitement des sorties. Ainsi, le modèle serait aussi simple d’utilisation que possible, sans toutefois que cela se fasse au détriment de ses performances et de sa flexibilité.

Le package IAM (version 2.0.2)

Ce qui suit va être une description par l’exemple des outils contenus dans la version 2.0.2 du package IAM. Il faut garder à l’esprit que ce package étant encore en cours de développement, certains des descriptifs présentés ici pourront devenir obsolètes dans les prochaines versions. Ajoutons que toute cette partie suppose une connaissance minimale du logiciel R (installation d’un package, utilisation de la fenêtre de commande,…).

Installation et chargement du package

L’installation du package IAM se fait de la même manière que tout autre package du CRAN, à la différence que le dépôt doit être précisé. D’autres méthodes d’installations sont développées dans le README.md du gitlab hébergeant le code source. Ces méthodes peuvent être utiles dans le cas d’installation de versions précédentes ou en cours de développement actif.

install.packages("IAM", repos = "https://ifremer-iam.r-universe.dev")

Après avoir installé le package IAM, l’instruction suivante va charger le package en session, donnant accès à tous les outils de modélisation :

library(IAM)

On peut vérifier que le package est bien installé en tapant :

help(IAM) # alternative : ?IAM
help(package = IAM)

Ces commandes permettend d’accéder à l’aide du package, avec une aide détaillée pour chaque fonction. S’y ajoute également l’ensemble des méthodes et des classes d’objets dorénavant accessibles.

Importation des paramètres (IAM.input)

La package intègre un fichier exemple de paramétrage qui va permettre d’illustrer le fonctionnement des procédures d’importation. La fonction IAM_example() renvoie le chemin du fichier d’exemple choisis dans le package IAM. Il s’agit de données brutes au format .xlsx ou .RData.

Ces données brutes sont constituées d’un fichier .xlsx, d’une fichier .RData contenant des informations pour une espèce SS3 ainsi qu’un dossier fleet/ contenant les informations sur les structures de coûts de plusieurs flotilles types.

IAM_example("inputFile.xlsx") # attention ici il s'agit d'un fichier brut.
# ce fichier est accessible a cette adresse pour être lu et modifié au besoin
list.files(IAM_example(file = "."), recursive = TRUE) 
# listes des fichiers accessibles avec IAM_example()

Le package contient également des objets intermédiaires issus des différentes fonctions. On peut accéder à la liste des fichiers d’exemples et leur documentation avec les commandes suivantes :

data(package = "IAM")

La méthode IAM.input() sert à l’importation des paramètres d’entrée bruts du modèle, et retourne un objet de classe iamInput regroupant de manière organisée toute ces données. Elle prend pour argument principal le chemin du fichier .xlsx à importer, complété par t_init l’instant initial, et nbStep le nombre de pas de temps désiré pour la simulation.

Dans le cadre de cet exemple, il faut cependant noter quelques modifications. En effet ici les flotilles ne sont pas comprises dans le fichier .xlsx et sont donc à aller chercher dans un dossier flottille avec l’argument folderFleet.

De même, une espèce décrite dans le fichier de paramètrage utilise un modèle de dynamique dit SS3, et les informations sont donc introduites à ce moment là. Il s’agit de mortalité définies par saisons.

On procède alors à l’importation de la manière suivante (attention, cela peut prendre quelques secondes selon le nombre de flottilles):

load(IAM_example("IAM_SS3_2009.RData"))

IAM_input_2009 <- IAM::IAM.input(
  fileIN = IAM_example("inputFile.xlsx"),
  t_init = 2009, nbStep = 12, folderFleet = IAM_example("fleets"),
  # elements 
  Fq_i = list(DAR = iniFq_i), iniFq_i = list(DAR = iniFq_i),
  Fq_fmi = list(DAR = iniFq_fmi), iniFq_fmi = list(DAR = iniFq_fmi),
  FqLwt_i = list(DAR = iniFqLwt_i), iniFqLwt_i = list(DAR = iniFqLwt_i),
  FqLwt_fmi = list(DAR = iniFqLwt_fmi), iniFqLwt_fmi = list(DAR = iniFqLwt_fmi),
  FqDwt_i = list(DAR = iniFqDwt_i), iniFqDwt_i = list(DAR = iniFqDwt_i),
  FqDwt_fmi = list(DAR = iniFqDwt_fmi), iniFqDwt_fmi = list(DAR = iniFqDwt_fmi),
  Nt0s1q = list(DAR = Nt0s1q), Ni0q = list(DAR = Ni0q),
  iniNt0q = list(DAR = iniNt0q), matwt = list(DAR = mat_morphage)
)

L’objet résultant (ici IAM_input_2009) de classe iamInput possède une structure fixe spécifique, composée d’éléments appelés “slots” et que l’on peut distinguer de cette façon :

slotNames(IAM_input_2009)
#> [1] "desc"         "specific"     "historical"   "input"        "scenario"    
#> [6] "stochastic"   "optimization"

Le slot “desc” est un simple descripteur permettant de caractériser l’objet ; c’est un paramètre optionnel de la fonction IAM.input. Le slot “specific” est constitué des descriptifs des dimensions du modèle qui vont conditionner la structure des variables. Le slot “historical” regroupe les données antérieures à l’instant initial t_init. Les slots “scenario” et “stochastic” intègrent les paramètres définis dans les feuillets correspondants. Enfin, le slot principal “input” rassemble les données initiales injectées dans le modèle. Il est composé d’un élément “Fleet” et d’un élément par espèce modélisée, ces derniers possédant la même structure. Au final, ce slot rassemble toutes les informations renseignées dans les feuillets “Stock”, “Flottille” et “Market”, ainsi que les matrices “fm”, “mm” et “icat”. Voici quelques exemples permettant d’accéder aux données de cet objet (l’accès aux slots se fait par objet@slot, l’accès aux éléments d’un slot par slot$élément) :

names(IAM_input_2009@specific)
#>  [1] "Species"   "StaticSpp" "AllSpp"    "Fleet"     "Metier"    "MetierEco"
#>  [7] "Ages"      "Cat"       "t_init"    "NbSteps"   "times"     "Q"        
#> [13] "S"
names(IAM_input_2009@input)
#>  [1] "ARC"   "COR"   "DAR"   "GAR"   "GLY"   "HER"   "MAH"   "DOR"   "PAV"  
#> [10] "INO"   "TUL"   "PAM"   "MON"   "OED"   "HAY"   "FET"   "RHO"   "IPH"  
#> [19] "THY"   "OCH"   "VAU"   "ZZZ"   "Fleet"
IAM_input_2009@input$COR$wStock_i
#>     2     3     4     5     6     7   +gp 
#> 0.200 0.252 0.302 0.373 0.394 0.405 0.555 
#> attr(,"DimCst")
#> [1] 0 0 7 0
attributes(IAM_input_2009@input$COR$wStock_i)$DimCst[3]
#> [1] 7

On peut ici noter l’attribut DimCst associé à la variable wStock_i . Chaque variable d’entrée insérée dans le slot input est affectée de cet attribut qui définit sa dimension : la première composante est la dimension flottille (0 signifie “pas de dimension”), la seconde est la dimension métier, la troisième est la dimension âge/catégorie, et la quatrième est la dimension temporelle. Dans l’exemple précédent, la variable se décline uniquement suivant la dimension “âge”, qui comprend pour l’espèce considérée 7 modalités. Cette attribution systématique permet au modèle de gérer les incompatibilités de dimensions entre les variables et de considérer plusieurs niveaux de définition pour une même variable.

Afin de simplifier l’utilisation de cette classe d’objets, une méthode summary() a été implémentée qui permet d’avoir un aperçu rapide :

summary(IAM_input_2009)
#> My Input (IAM input) :
#> Simulation of 3 dynamic species, 19 static species and 7 fleet
#> Simulation start in 2009 and end in 2020 (12 steps)
#> 
#> -----------------------------------------
#> Dynamic Species | Model |     Ages (nb) |
#>             ARC |   XSA | 0 to +gp (21) |
#>             COR |   XSA | 2 to +gp ( 7) |
#>             DAR |   SS3 | 0 to +gp (16) |
#> -----------------------------------------
#>                   Fleet |    nbv   |
#>                    Alis |    24    |
#>                   Antea |    36    |
#>                Atalante |    15    |
#>                Haliotis |     5    |
#>         Marion_Dufresne |     9    |
#>            Pourquoi_pas |    18    |
#>                Thalassa |    60    |

Constitution des arguments (IAM.args)

La méthode IAM.args() prend en paramètre un objet de classe iamInput et permet à l’utilisateur de fixer les caractéristiques de la simulation à opérer. Une interface de paramétrage s’affiche, et la validation renvoie un objet de classe iamArgs définissant les choix de pilotage du modèle.

IAM_argum_2009 <- IAM.args(IAM_input_2009)

L’instruction va provoquer l’affichage d’une interface de paramétrage comportant 5 parties distinctes, chacune activant ou/et paramétrant une partie spécifique du modèle.

• Recruitment : ce panneau de commande de type “tabbed notebook” permet de définir l’intégration de la variabilité dans le modèle en caractérisant le recrutement considéré dans la simulation. Il y a un onglet par espèce modélisée, chacun donnant accès à un choix de paramètres similaires. On pourra soit opter pour un recrutement généré par une relation stock-recrutement (activer alors le panneau en cochant “Stock Recrutement Model”, soit simuler un recrutement par tirage aléatoire dans un historique ou une loi de probabilité (cocher “StockSim”). Dans le premier cas, 5 paramètres sont à définir : le type de relation stock-recrutement, les paramètres de la relation (3 au maximum), et l’écart-type du bruit gaussien centré additionnel. Les relations sont décrites dans le tableau suivant :

  Relation Stock-Recrutement	Formulation (\(\sigma\) est le bruit gaussien)
  Mean	\(rec \sim a + \sigma\)
  Hockey Stick	si \(ssb \leq b\) : \(rec \sim a \cdot ssb + \sigma\) sinon : \(rec \sim a \cdot b + \sigma\)
  Beverton-Holt	\(rec \sim \frac{ a \cdot ssb }{ b+ssb } + \sigma\)
  Ricker	\(rec \sim a \cdot ssb \cdot e^{-b \cdot ssb} + \sigma\)
  Shepherd	\(rec \sim \frac{a \cdot ssb}{1+ (\frac{ssb}{b})^{c}} + \sigma\)
  Hockey Stick Quadratic	si \(ssb \leq b \cdot (1-c)\) : \(rec \sim a \cdot ssb + \sigma\) si \(ssb \geq b \cdot (1+c)\) : \(rec \sim a \cdot b + \sigma\) sinon : \(rec \sim a \cdot (ssb-\frac{( ssb - b \cdot (1-c))^{2}}{4 \cdot b \cdot c}) + \sigma\)
  Hockey Stick Smooth	\(rec \sim a \cdot \{ssb+ \sqrt{b^{2}+g}-\sqrt{(ssb-b)^{2}+g}\} + \sigma\) avec \(g=0.001\)

  Il est possible d’annuler l’effet aléatoire en mettant la variable \(\sigma\) à 0 (pas de variance, donc pas de variabilité). Précisons aussi que le recrutement s’exprime ici en nombre d’individus. La deuxième possibilité est de considérer le recrutement comme étant la réalisation d’un tirage aléatoire. Trois options sont alors envisageables :

  • l’option 1 permet d’effectuer un tirage aléatoire dans l’historique de recrutement renseigné dans le feuillet “Stochasticité” du fichier de paramétrage, de manière indépendante (avec toutefois la pondération des probabilités spécifiée dans le fichier .xlsx).

  • l’option 2 est similaire à l’option 1, à la différence que le tirage ne sera pas indépendant. Pour chaque instant de la simulation, un seul tirage sera effectué pour toutes les espèces d’option 2 de recrutement pour déterminer un instant commun de l’historique à considérer. Notons que ce type de tirage impliquera seulement l’intersection des historiques pour les espèces concernées.

  • enfin, l’option 3 offre la possibilité de simuler le recrutement d’une espèce comme étant la réalisation d’une variable aléatoire de loi prédéterminée. Cette loi devra également être préalablement définie au sein du feuillet “Stochasticité” du fichier de paramètres.

• Replicates : cette partie de l’interface permet de piloter le module de réplication. Pour activer/désactiver le module, cocher “activate”. Une fois le module activé, on peut paramétrer le nombre d’itérations à opérer, et choisir les variables en sortie. Cette option permet de limiter la taille des résultats de simulations qui peuvent devenir très volumineux si on multiplie inconsidérément le nombre de réplicats. Ce sera surtout le cas avec des variables à haut niveau de précision telles que L_efmit.

• Scenario : cette partie de l’interface permet de choisir le scénario à simuler, ce dernier étant caractérisé dans le feuillet “Scénario” du fichier de paramétrage. Pour activer/désactiver le module, cocher “activate”. Une fois le module activé, un scénario devra être sélectionné dans la liste (par définition, un scénario Statu Quo impliquera la désactivation du module). Afin de simplifier la mise en oeuvre des simulations et la gestion des sorties du modèle, on ne peut simuler qu’un seul scénario par envoi. A noter que ces scénarios sont plus difficiles à régler et demandent une bonne compréhension du modèle par rapport à l’utilisation de scénario par la partie “Management” du modèle et les scénarios de TAC.

• Management : le module “Management” peut être piloté intégralement par cette composante de l’interface pour les scénarios de TAC totaux. Un paramétrages de scénarios TAC par flottilles par exemple requiert de paramétrer la fonctions IAM.model() et fait l’objet d’une autre vignette. Tout comme pour les deux précédents contrôles, on activera le module en cochant “activate”, permettant ainsi l’accès aux champs de paramètres à renseigner suivants :

  • Control : permet de spécifier sur quelle variable d’effort agir afin d’atteindre les objectifs de gestion (pour le moment, laisse le choix entre le nombre de navires et le nombre de jours de mer).

  • Target : variable sur laquelle porte les objectifs définis (3 options : atteinte du TAC, atteinte du Fbar, ou atteinte du TAC jusqu’à atteindre le Fbar, puis atteinte du Fbar).

  • Bouton TAC/Fbar : permet de renseigner les valeurs-objectifs de TAC et de Fbar pour l’espèce en question, sur l’intervalle de temps spécifié dans le paramétrage (une cellule par pas de temps). Il est conseillé de renseigner toutes les cellules de la table, en particulier pour une cible de type 3 (voir plus haut). La validation des valeurs s’opère à la fermeture de la fenêtre.

  • Species : espèce sur laquelle porte la mesure de gestion (à choisir entre toutes les espèces modélisées)

  • Type : multiplicatif ou additif.

  • Delay : délai d’application de la mesure de gestion (autrement dit, temps d’attente avant la mise en activation du module).

  • Update : définit si l’ajustement s’opère à chaque fois sur les valeurs initiales des variables, ou sur les valeurs mises à jour. (NB: cette option n’impacte que sur la manière de quantifier les ajustements, et ne revêt de l’importance que dans des cadres d’utilisation très spécifiques).

  • Upper bound / Lower bound : bornes de l’intervalle d’application de la procédure d’optimisation. Un intervalle restreint permet de maximiser le temps de calcul, mais fait prendre le risque de ne pas trouver de solution. Ces valeurs sont fortements dépendantes du type de gestion réglé. A utiliser avec précaution.

  • Bouton Eff table : effort maximum par flottille.

  • Bouton mFm table : permet de renseigner les pondérations (décimales) par flottille utilisées durant le processus d’ajustement (une cellule par classe de flottille). Cette pondération permet de paramétrer la distribution d’effort concédée par chaque flottille afin d’atteindre l’objectif désiré. Un poids nul signifiera que la flottille en question conservera son effort initial. Un poids p signifiera que la variation de l’effort consentie par la flottille pour atteindre au final la valeur objectif sera p fois plus importante que celle des flottilles de poids unité (attention : tout ceci s’applique relativement au signe de variation global, qui peut être contrôlé par le biais des bornes supérieures et inférieures préalablement définies). Des poids de signes opposés peuvent être utilisés pour simuler des variations contraires selon les flottilles.

• Economic : la dernière phase de paramétrisation concerne le modèle économique. La plupart des paramètres ici décrits peuvent être retrouvés dans le tableau de mise en équation du modèle économique en annexe de ce document.

  • perscCalc : Mode de calcul de la variable “coût du personnel”
    • 0 : la variable est supposée constante
    • 1 : relation linéaire avec rtbs et donnée cshr disponible
    • 2 : relation linéaire avec rtbs et donnée cshr indisponible
  • Discound rate (dr) (Taux d’actualisation): Attention, le taux est en décimal, pas en pourcentage. Pour 4% d’actualisation, il faut rentrer la valeur 0,04. Ce taux d’actualisation va s’appliquer en sortie du modèle à une sélection de variables économiques principales, qui seront donc disponibles en 2 versions, actualisée et non actualisée. Ces variables sont les suivantes : rtbs_f, cs_f, gva_f, gcf_f, ps_f et sts_f.

Une fois la validation des arguments effectuée en cliquant sur “OK”, un objet de classe iamArgs est retourné, intégrant tous les arguments qui vont conditionner les processus mis en œuvre pendant la phase de simulation. Afin de simplifier l’utilisation de cette classe d’objets, une méthode summary() a été implémentée qui permet d’avoir un aperçu rapide

summary(IAM_argum_2009)
#> My Input (IAM argument) :
#> Simulation of 3 dynamic species, 19 static species and 7 fleet
#> Simulation start in 2009 and end in 2020 (12 steps)
#> 
#> =======================================================================================
#>   SR module  |               Stock Recruitment             |      Noise       | Proba |
#> ---------------------------------------------------------------------------------------
#>     Species  |    function  :  param A ; param B ; param C |  Type :    sd    |  Type |
#>    ARC (XSA) |          Mean 3.641e+07  0.00e+00  0.00e+00 |  Norm | 0.00e+00 |   .   |
#>    COR (XSA) |          Mean 1.893e+07  0.00e+00  0.00e+00 |  Norm | 0.00e+00 |   .   |
#>    DAR (SS3) | not activated 0.000e+00  0.00e+00  0.00e+00 |  Norm | 0.00e+00 |   .   |
#> ---------------------------------------------------------------------------------------
#> 
#>  The Gestion module is not active.
#> 
#> ============================================================
#> Economic : PerscCalc = 0 ; dr = 0.000 | No replicates      |
#> ------------------------------------------------------------
#> 
#>  The Scenario module is not active.
names(IAM_argum_2009@arguments)
#> [1] "Recruitment" "Replicates"  "Scenario"    "Gestion"     "Eco"

On peut modifier l’objet déjà existant utilisant des fonctions spécifiques et les valeurs voulues. Mais ceci suggère une bonne connaissance de R et un risque non négligeable d’entamer la structure de l’objet. Par exemple, pour mettre en oeuvre la module Gestion et modifier les variables économiques :

# Modify Gestion
IAM_argum_2009 <- IAM.editArgs_Gest(
  IAM_argum_2009, active = TRUE, control = "Nb trips", target = "Fbar",
  espece = "DAR", type = "x")
# Modify Eco
IAM_argum_2009 <- IAM.editArgs_Eco(IAM_argum_2009, dr = 0.04, perscCalc = 3)
# Check if Gestion is active
summary(IAM_argum_2009)
#> My Input (IAM argument) :
#> Simulation of 3 dynamic species, 19 static species and 7 fleet
#> Simulation start in 2009 and end in 2020 (12 steps)
#> 
#> =======================================================================================
#>   SR module  |               Stock Recruitment             |      Noise       | Proba |
#> ---------------------------------------------------------------------------------------
#>     Species  |    function  :  param A ; param B ; param C |  Type :    sd    |  Type |
#>    ARC (XSA) |          Mean 3.641e+07  0.00e+00  0.00e+00 |  Norm | 0.00e+00 |   .   |
#>    COR (XSA) |          Mean 1.893e+07  0.00e+00  0.00e+00 |  Norm | 0.00e+00 |   .   |
#>    DAR (SS3) | not activated 0.000e+00  0.00e+00  0.00e+00 |  Norm | 0.00e+00 |   .   |
#> ---------------------------------------------------------------------------------------
#> 
#> =============================================================================
#>                      Gestion Module                                         | 
#> -----------------------------------------------------------------------------
#>     Species  |   control  |    target | delay | typeG | update |   bounds   |
#>    DAR (SS3) |   Nb trips |      Fbar |    2  |   x   |   yes  |   0 :    0 |
#> -----------------------------------------------------------------------------
#>    TAC : NA NA NA NA NA NA NA NA NA NA NA NA 
#>   FBAR : NA NA NA NA NA NA NA NA NA NA NA NA 
#> ----------------------------------------------------------------------------
#> 
#> ============================================================
#> Economic : PerscCalc = 3 ; dr = 0.040 | No replicates      |
#> ------------------------------------------------------------
#> 
#>  The Scenario module is not active.
# Desactivate Gestion
IAM_argum_2009 <- IAM.editArgs_Gest(IAM_argum_2009, active = FALSE)

Mais la procédure la plus simple pour corriger un objet est de reprendre l’interface au stade de la validation, et d’effectuer directement les corrections. Pour cela, il suffit de rappeler la méthode IAM.args(), mais non plus affectée à un objet de paramétrage initial de classe iamInput, mais plutôt à l’objet qu’on désire modifier. On tape donc :

IAM_argum_2009 <- IAM.args(IAM_argum_2009)

Une interface reprenant tous les arguments auparavant validés s’ouvre, permettant la correction, la validation, et ainsi la mise à jour de l’objet IAM_argum_2009 en sortie.

Simulation (IAM.model)

Une fois les deux principaux composants du paramétrage obtenus, la mise en route de la simulation est très simple : la méthode IAM.model() appelle l’objet de classe iamArgs et l’objet de classe iamInput et restitue les résultats de la simulation dans un objet de classe iamOutput, ou de classe iamOutputRep si le module de réplication est activé.

IAM_out_2009 <- IAM.model(IAM_argum_2009,IAM_input_2009)
class(IAM_out_2009)
#> [1] "iamOutput"
#> attr(,"package")
#> [1] "IAM"

Toutes les sorties du modèle sont entreposées dans 2 slots de l’objet IAM_out_2009. Un slot outputSp réunit toutes les variables définies par espèce modélisée (sorties du modèle biologique principalement), et un autre slot output rassemble les variables sans dimension espèce (les variables économiques). L’accès aux variables est illustré ci-dessous :

slotNames(IAM_out_2009)
#> [1] "desc"      "arguments" "specific"  "outputSp"  "output"
names(IAM_out_2009@outputSp)
#>   [1] "F"              "Fr"             "Fothi"          "Fbar"          
#>   [5] "Z"              "N"              "B"              "SSB"           
#>   [9] "C"              "Ctot"           "Y"              "Ytot"          
#>  [13] "D"              "Li"             "Lc"             "Ltot"          
#>  [17] "L_et"           "L_pt"           "P"              "GVL_f_m_e"     
#>  [21] "GVLcom_f_m_e"   "GVLst_f_m_e"    "statY"          "statL"         
#>  [25] "statD"          "statP"          "statGVL_f_m"    "statGVLcom_f_m"
#>  [29] "statGVLst_f_m"  "PQuot"          "TradedQ"        "F_S1M1"        
#>  [33] "F_S1M2"         "F_S1M3"         "F_S1M4"         "F_S2M1"        
#>  [37] "F_S2M2"         "F_S2M3"         "F_S2M4"         "F_S3M1"        
#>  [41] "F_S3M2"         "F_S3M3"         "F_S3M4"         "F_S4M1"        
#>  [45] "F_S4M2"         "F_S4M3"         "F_S4M4"         "Fr_S1M1"       
#>  [49] "Fr_S1M2"        "Fr_S1M3"        "Fr_S1M4"        "Fr_S2M1"       
#>  [53] "Fr_S2M2"        "Fr_S2M3"        "Fr_S2M4"        "Fr_S3M1"       
#>  [57] "Fr_S3M2"        "Fr_S3M3"        "Fr_S3M4"        "Fr_S4M1"       
#>  [61] "Fr_S4M2"        "Fr_S4M3"        "Fr_S4M4"        "Z_S1M1"        
#>  [65] "Z_S1M2"         "Z_S1M3"         "Z_S1M4"         "Z_S2M1"        
#>  [69] "Z_S2M2"         "Z_S2M3"         "Z_S2M4"         "Z_S3M1"        
#>  [73] "Z_S3M2"         "Z_S3M3"         "Z_S3M4"         "Z_S4M1"        
#>  [77] "Z_S4M2"         "Z_S4M3"         "Z_S4M4"         "N_S1M1"        
#>  [81] "N_S1M2"         "N_S1M3"         "N_S1M4"         "N_S2M1"        
#>  [85] "N_S2M2"         "N_S2M3"         "N_S2M4"         "N_S3M1"        
#>  [89] "N_S3M2"         "N_S3M3"         "N_S3M4"         "N_S4M1"        
#>  [93] "N_S4M2"         "N_S4M3"         "N_S4M4"         "DD_efmi"       
#>  [97] "DD_efmc"        "LD_efmi"        "LD_efmc"        "statDD_efm"    
#> [101] "statLD_efm"     "statLDst_efm"   "statLDor_efm"   "oqD_ef"        
#> [105] "oqD_e"          "oqDstat_ef"     "TACtot"         "TACbyF"        
#> [109] "PQuot_conv"     "diffLQ_conv"
names(IAM_out_2009@output)
#>  [1] "nbv_f"              "effort1_f"          "effort2_f"         
#>  [4] "nbv_f_m"            "effort1_f_m"        "effort2_f_m"       
#>  [7] "GVLtot_f_m"         "GVLav_f_m"          "GVLtot_f"          
#> [10] "GVLav_f"            "NGVLav_f_m"         "NGVLav_f"          
#> [13] "ET_f_m"             "cnb_f_m"            "cnb_f"             
#> [16] "rtbs_f_m"           "rtbs_f"             "rtbsAct_f"         
#> [19] "cshrT_f_m"          "cshrT_f"            "ncshr_f"           
#> [22] "ocl_f"              "cs_f"               "csAct_f"           
#> [25] "csTot_f"            "gva_f"              "gvaAct_f"          
#> [28] "gvamargin_f"        "gva_FTE_f"          "ccw_f"             
#> [31] "ccwCr_f"            "wageg_f"            "wagen_f"           
#> [34] "wageg_FTE_f"        "wageg_h_f"          "gp_f"              
#> [37] "gpAct_f"            "gpmargin_f"         "ncf_f"             
#> [40] "np_f"               "npmargin_f"         "prof_f"            
#> [43] "npmargin_trend_f"   "ssTot_f"            "ps_f"              
#> [46] "psAct_f"            "sts_f"              "stsAct_f"          
#> [49] "BER_f"              "CR_BER_f"           "fuelEff_f"         
#> [52] "ratio_fvol_gva_f"   "ratio_gp_gva_f"     "ratio_GVL_K_f"     
#> [55] "ratio_gp_K_f"       "RoFTA_f"            "ROI_f"             
#> [58] "ratio_np_K_f"       "ratio_GVL_cnb_ue_f" "YTOT_fm"           
#> [61] "reconcilSPP"        "quotaExp_f"         "allocEff_f_m"      
#> [64] "GoFish"

Dans le cas d’un objet de classe iamOutputRep, chaque variable est une liste de n éléments, avec n le nombre de réplicats.

# Activate replicates
IAM_argumRep_2009 <- IAM.editArgs_Rep(IAM_argum_2009, n = 2)

IAM_outRep_2009 <- IAM.model(IAM_argumRep_2009,IAM_input_2009)
class(IAM_outRep_2009)
#> [1] "iamOutputRep"
#> attr(,"package")
#> [1] "IAM"
length(IAM_outRep_2009@outputSp$F)
#> [1] 2
names(IAM_outRep_2009@outputSp$F[[1]])
#> [1] "ARC" "COR" "DAR"
names(IAM_outRep_2009@outputSp$F[[2]])
#> [1] "ARC" "COR" "DAR"

Mise en forme des sorties (IAM.format & IAM.format_quant)

La méthode IAM.format est une fonction de formatage appliquée aux objets iamOutput . Elle va permettre la conversion d’une variable multidimensionnelle en une table de type “data.frame” (format facilitant la création de graphiques adaptés à ce type de variables)

Cette fonction prend également en entrée le nom d’une ou plusieurs variables à extraire, un nom de simulation et un numero qui pourront servir plus tard pour aggréger plusieurs simulations ensemble.

On note qu’une variable spéciale nommée "summary" permet d’extraire d’un seul coup quelques variables biologiques et économiques.

# Extraction d'une variable
statu_quo_tbl_Fbar <- IAM.format(IAM_out_2009, name = "Fbar", 
                                 sim_name = "statu_quo", n = 1)
head(statu_quo_tbl_Fbar)
#> # A tibble: 6 × 9
#>   sim_name      n variable species fleet metier age    year value
#>   <chr>     <dbl> <chr>    <chr>   <chr> <chr>  <chr> <dbl> <dbl>
#> 1 statu_quo     1 Fbar     ARC     NA    NA     NA     2009 0.122
#> 2 statu_quo     1 Fbar     ARC     NA    NA     NA     2010 0.122
#> 3 statu_quo     1 Fbar     ARC     NA    NA     NA     2011 0.122
#> 4 statu_quo     1 Fbar     ARC     NA    NA     NA     2012 0.122
#> 5 statu_quo     1 Fbar     ARC     NA    NA     NA     2013 0.122
#> 6 statu_quo     1 Fbar     ARC     NA    NA     NA     2014 0.122
# Extraction de plusieurs variables
statu_quo_tbl_summary <- IAM.format(IAM_out_2009, name = "summary", 
                                    sim_name = "statu_quo", n = 1)
unique(statu_quo_tbl_summary$variable)
#>  [1] "Fbar"      "SSB"       "L_et"      "N"         "nbv_f"     "effort1_f"
#>  [7] "effort2_f" "GVLav_f"   "gva_f"     "gp_f"      "wageg_f"   "wagen_f"

Ce format de table long permet ensuite l’utilisation d’outils pour trier et éventuellement produire les tables dans un format large.

library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union
library(tidyr)
library(purrr)
library(magrittr)
#> 
#> Attaching package: 'magrittr'
#> The following object is masked from 'package:purrr':
#> 
#>     set_names
#> The following object is masked from 'package:tidyr':
#> 
#>     extract

# Extraction du SSB
statu_quo_tbl_summary %>%
  dplyr::filter( species == "COR", variable == "SSB") %>% # trie des lignes
  discard(~all(is.na(.x))) %>% # retire les colonnes vides (NA)
  # Ligne optionnelle pour enlever les colonnes identiques.
  # discard( ~ n_distinct(.) == 1) %>% 
  pivot_wider(names_from = year, values_from = value) # mise en forme horizontale
#> # A tibble: 1 × 16
#>   sim_n…¹     n varia…² species `2009` `2010` `2011` `2012` `2013` `2014` `2015`
#>   <chr>   <dbl> <chr>   <chr>    <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>
#> 1 statu_…     1 SSB     COR     10426. 11347. 12051. 12523. 12820. 13033. 13158.
#> # … with 5 more variables: `2016` <dbl>, `2017` <dbl>, `2018` <dbl>,
#> #   `2019` <dbl>, `2020` <dbl>, and abbreviated variable names ¹​sim_name,
#> #   ²​variable


# Table de gp_f
statu_quo_tbl_summary %>%
  dplyr::filter(variable == "gp_f") %>% # trie des lignes
  discard(~all(is.na(.x))) %>% # retire les colonnes vides (NA)
  # Ligne optionnelle pour enlever les colonnes identiques.
  discard( ~ n_distinct(.) == 1) %>% 
  pivot_wider(names_from = year, values_from = value) # mise en forme horizontale
#> # A tibble: 7 × 13
#>   fleet   `2009`  `2010`  `2011`  `2012`  `2013`  `2014`  `2015`  `2016`  `2017`
#>   <chr>    <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>
#> 1 Alis   -3.10e7 -3.10e7 -3.10e7 -3.10e7 -3.10e7 -3.10e7 -3.10e7 -3.10e7 -3.10e7
#> 2 Antea  -4.75e7 -4.75e7 -4.75e7 -4.75e7 -4.75e7 -4.75e7 -4.75e7 -4.75e7 -4.75e7
#> 3 Atala… -1.18e7 -1.18e7 -1.18e7 -1.18e7 -1.18e7 -1.18e7 -1.18e7 -1.18e7 -1.18e7
#> 4 Halio… -6.83e5 -6.86e5 -6.92e5 -6.92e5 -6.87e5 -6.72e5 -6.54e5 -6.38e5 -6.24e5
#> 5 Mario… -6.24e6 -6.26e6 -6.25e6 -6.23e6 -6.23e6 -6.24e6 -6.24e6 -6.25e6 -6.25e6
#> 6 Pourq… -1.66e7 -1.66e7 -1.66e7 -1.66e7 -1.66e7 -1.66e7 -1.66e7 -1.66e7 -1.66e7
#> 7 Thala… -3.21e7 -3.21e7 -3.21e7 -3.21e7 -3.21e7 -3.21e7 -3.21e7 -3.21e7 -3.20e7
#> # … with 3 more variables: `2018` <dbl>, `2019` <dbl>, `2020` <dbl>

Dans le cas d’une liste d’objet de classe iamOuput, il est possible d’extraire les variables, de concaténer et d’ensuite calculer une table résumée ne présentant que les quantiles d’interêt. Cela permet d’alleger les sorties du modèle et de les manipuler plus simplement lors de la production de représentations graphiques.

res1 <- IAM.format(IAM_out_2009, c("SSB"), n = 1) %>%
 dplyr::filter(species == "ARC", year <= 2011)
# Je modifie légérement les données pour avoir des quantiles écartés.
res2 <- mutate(res1, n = 2, value = value + rnorm(1, sd = 100))

# On peut associer les données extraites avec rbind.
res <- rbind(res1, res2)

IAM.format_quant(res, probs = c(0.025, 0.975), select_indiv = 2) %>%
  discard(~all(is.na(.x)))
#> # A tibble: 3 × 8
#>   variable species  year quant1 quant2 median  value  nsim
#>   <chr>    <chr>   <dbl>  <dbl>  <dbl>  <dbl>  <dbl> <int>
#> 1 SSB      ARC      2009 18695. 18722. 18709. 18695.     2
#> 2 SSB      ARC      2010 17963. 17989. 17976. 17962.     2
#> 3 SSB      ARC      2011 17193. 17219. 17206. 17192.     2

A noter que des colonnes seront souvent remplies de valeurs manquantes car peu de variables sont définies sur toutes les dimensions d’IAM. Cependant, il vaut mieux conserver ces colonnes jusqu’au dernier moment afin de pouvoir trier les données avec des fonctions génériques ou encore pouvoir utiliser rbind.

Représentations graphiques des sorties avec ggplot2

Les procédures graphiques ont été retirées du packages et se basent sur l’utilisation du package ggplot2. Ainsi, le format de table renvoyé par les fonctions IAM.format et IAM.format_quant sera requis pour constiturer la donnée à représenter.

Pour illustrer différentes représentations graphiques, on va générer plusieurs réplicats. Le premier sera similaire le cas de statu quo généré plus haut. On modifie le module de recrutement pour l’espèce “COR” afin d’ajouter un peu d’effets stochastiques. Un second scénario est simulé avec l’application de quotas. Le détails de ce genre de simulations est donné dans la vignette “Gestion_TAC”.

N = 5

# Add noise to COR recruitment
IAM_argum_2009@arguments$Recruitment$COR$wnNOISEmodSR <- 0.2
IAM_argum_2009@arguments$Recruitment$COR$noiseTypeSR <- 2 # Log-normal
IAM_argum_2009@arguments$Recruitment$COR$typeMODsr <- "Hockey-Stick"
IAM_argum_2009@arguments$Recruitment$COR$parAmodSR <- 2600
IAM_argum_2009@arguments$Recruitment$COR$parBmodSR <- 9700

# Simulation
sim_statu_quo <- replicate(N, {
  IAM::IAM.model(objArgs = IAM_argum_2009,  objInput = IAM_input_2009)
})
# Edition des arguments
IAM_argum_2009_TACnbv <- IAM.editArgs_Gest(
  IAM_argum_2009, active = TRUE, control = "Nb vessels", target = "TAC",
  espece = "COR", delay = 2, type = "x", bounds = c(1e7, -1), 
  tac = c(NA, NA, rep(3400, 10)))
# Simulation
sim_TACglob_nbv <- replicate(N, {
  IAM::IAM.model(objArgs = IAM_argum_2009_TACnbv,  
                 objInput = IAM_input_2009, mOTH = 1)
})

# Formatage
TACglobv_nbv_l <- lapply(1:N,  function(x) {
  IAM.format(sim_TACglob_nbv[[x]], name = "summary", 
             sim_name = "TAC global nbv", n = x)
})
Statuquo_l <- lapply(1:N,  function(x) {
  IAM.format(sim_statu_quo[[x]], name = "summary", 
             sim_name = "Statu quo", n = x)
})

TACvsSQ_5simuls <- do.call(rbind, c(Statuquo_l, TACglobv_nbv_l)) %>%
  IAM.format_quant(., probs = c(.025, .975))

Pour les sorties graphiques on aura besoin du package ggplot2. Cette dépendance est normalement installée en même temps que le package IAM. Ce package est très riche en terme de représentations graphiques, on pourra se référer à sa documentation pour plus de précisions.Un site repertorie également de nombreux exemples : https://r-graph-gallery.com/.

library(ggplot2)
library(magrittr) # utilisation du pipe %>%
library(dplyr) # utilisation de filtres

Voici quelques exemples de représentations graphiques disponibles pour les sortie d’IAM :

TACvsSQ_5simuls %>%
  # Filtrer de l'espece et de la variable cible
  dplyr::filter(species == "COR", variable == "Fbar") %>%
  ggplot(aes(x = year, y = median)) +
  facet_grid(. ~ sim_name, scales = "free_y") +
  geom_ribbon(aes(ymin = quant1, ymax = quant2), fill = "white", alpha = .4) +
  geom_line() + geom_point(size = .5) +
  guides(x = guide_axis(angle = 90)) + IAM_theme() +
  NULL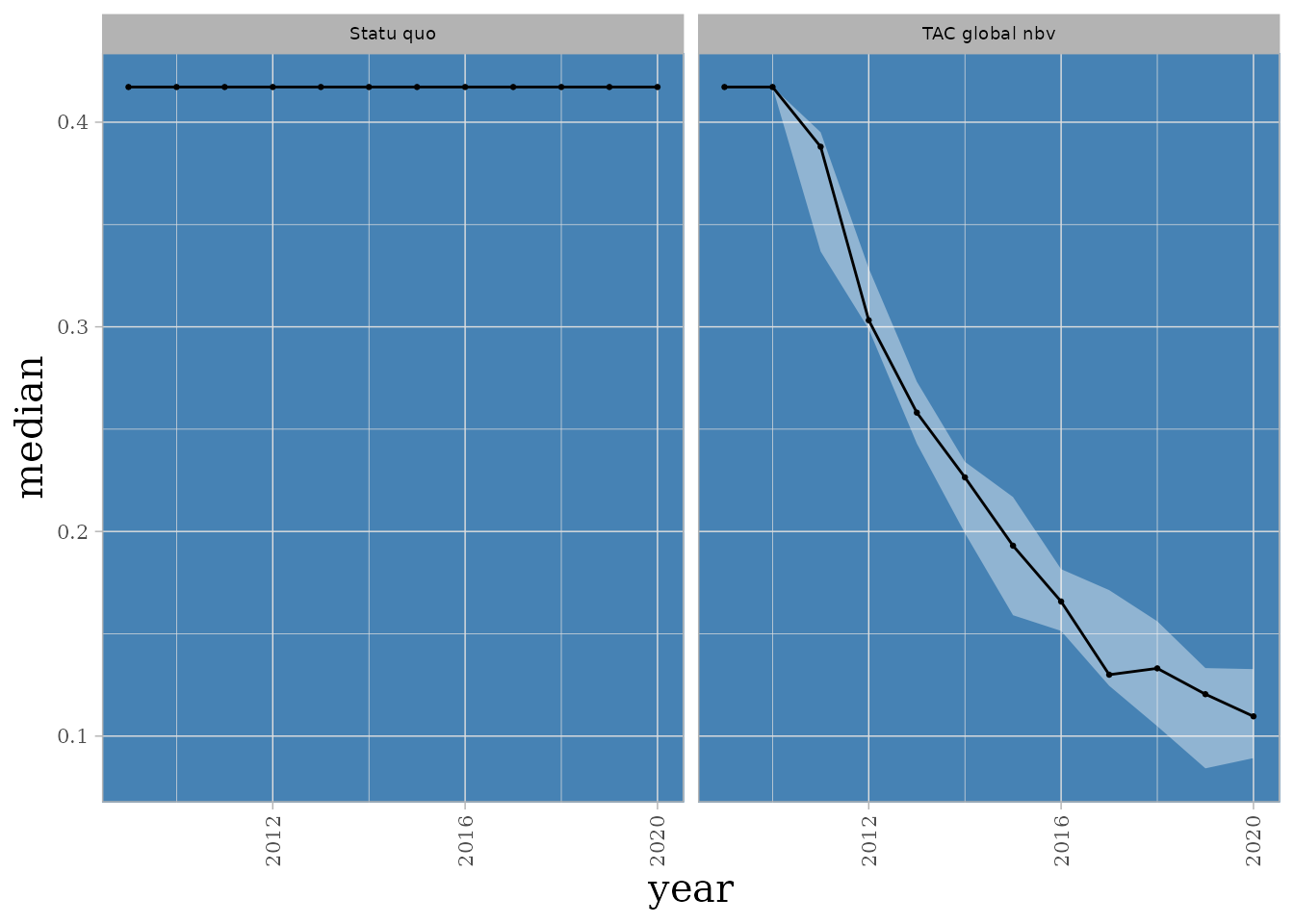

Evolution du Fbar dans le cas de l’espèce COR. 5 runs.

L’exemple précédent permet d’illustrer la comparaison du Fbar pour deux scénarios et une espèce donnée (“COR”). On peut observer l’enveloppe à droite qui est représente les deux quartiles entre lesquels on retrouve 95% des simulations.

On peut également représenter plusieurs variables comme ci-dessous les variables biologiques de l’espèce COR :

TACvsSQ_5simuls %>%
 dplyr::filter(species == "COR", variable %in% c("Fbar", "SSB", "L_et")) %>%
 ggplot(aes(x = year, y = median)) +
 facet_grid(variable ~ sim_name, scales = "free_y") +
 geom_ribbon(aes(ymin = quant1, ymax = quant2), fill = "white", alpha = .4) +
 geom_line() + geom_point(size = .5) +
 guides(x = guide_axis(angle = 90)) + IAM_theme() +
 NULL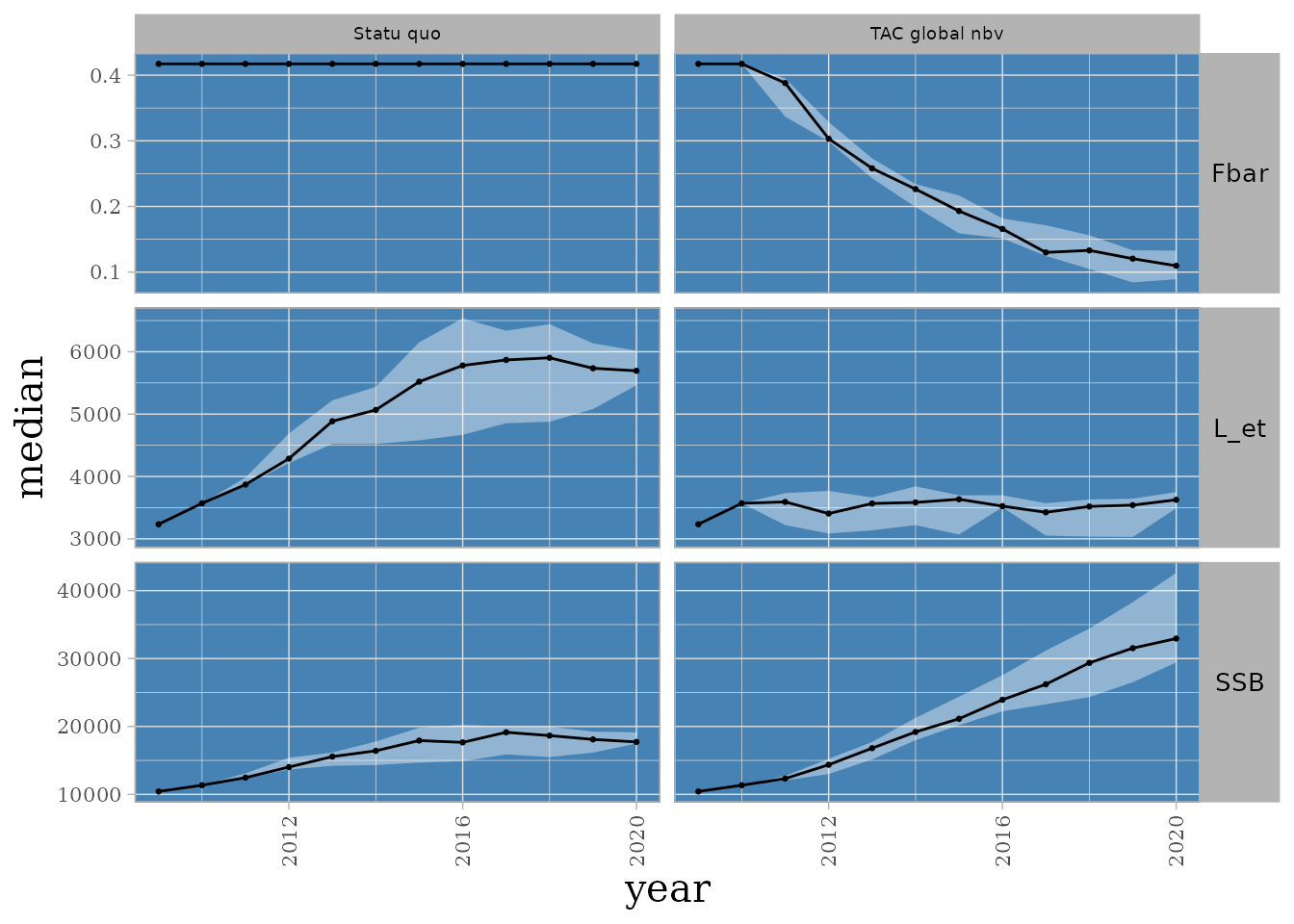

Evolution des variables biologiques dans le cas de l’espèce COR. 5 runs.

Enfin, on peut tout à fait intégrer plus de dimensions aux graphiques avec l’ajout de couleurs pour par exemple ici comparer deux scénarios par Flottilles et variables économiques :

TACvsSQ_5simuls %>%
 dplyr::filter(variable %in% c("GVLav_f", "nbv_f")) %>%
 ggplot(aes(x = year, y = median, color = sim_name)) +
 facet_grid(variable ~ fleet, scales = "free_y") +
 geom_ribbon(aes(ymin = quant1, ymax = quant2), fill = "white", alpha = .4) +
 geom_line() + geom_point(size = .5) +
 guides(x = guide_axis(angle = 90)) + IAM_theme() +
 scale_color_manual(values=c("darkred", "darkorange")) +
 theme(legend.position = "bottom") +
 NULL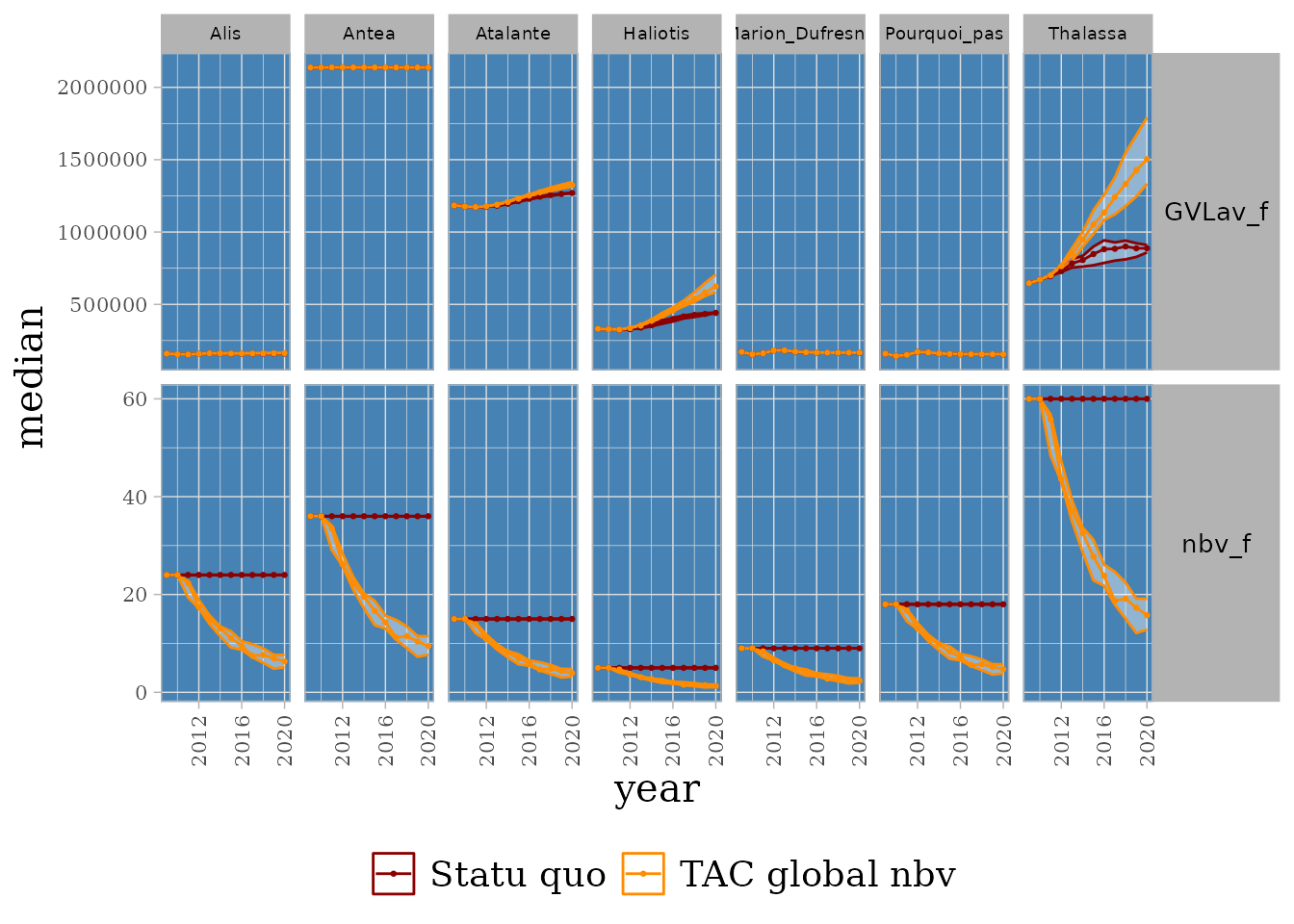

Evolution des variables économiques pour les flottilles modélisées. 5 runs.

Conseil de réplication

L’utilisation du package IAM prend tout son sens lors du lancement d’un même scénario répliqué de nombreuses fois. Cela permet de prendre en compte les problématiques stochastiques de certaines variables comme le recrutement. Ainsi, un même scénario peut être lancé plusieurs centaines de fois. Cette option est implémentée de base dans le package avec la classe IAMOutputRep, mais celle-ci est dépcréciée car ne permettant plus la réalisation de scénarios complexes.

Une autre alternative réside dans l’utilisation de code R pour forcer de grands nombres de réplicats, au détriment d’une plus grande place en mémoire. Notons tout de même que cela peut prendre un certain temps.

# Code non exécuté
library(IAM)
a <- Sys.time() # mesure du temps
nsim_statu_quo <- replicate(
  500,
  IAM::IAM.model(objArgs = IAM_argum_2009, objInput = IAM_input_2009)
)
b <- Sys.time() # mesure du temps
b - a # 1.17 min

Afin de gagner du temps, le package {parallel} permet d’effectuer les calculs sur un plus grand nombre de processeurs de l’ordinateurs. L’utilisation de ce package permet de réduire le temps de calcul pour un grand nombre de réplicats et est donc conseillé.

# Code non exécuté
library(parallel)
cl <- makeCluster(detectCores()-1)

clusterEvalQ(cl,library(IAM)) # charger les librairies dans le cluster.

c <- Sys.time() # mesure du temps
# rendre les objets disponibles pour le code
clusterExport(cl,c("IAM_argum_2009", "IAM_input_2009"))
# S'assurer de "seed" différentes pour chaque noeud.
clusterSetRNGStream(cl)
#... Simuler les réplicats ...
res <- parSapply(cl, 1:50, function(i,...) {
  IAM::IAM.model(objArgs = IAM_argum_2009, objInput = IAM_input_2009)
  } )
# Arreter le cluster
stopCluster(cl)
d <- Sys.time() # mesure du temps
d - c # 51 sec !!!

References

R Core Team. 2021. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.